In the realm of data analysis and predictive modeling, logistic regression is particularly renowned for its ability to handle binary outcomes, making it a go-to method for researchers and data scientists alike. As we delve into the intricacies of it, we will uncover its fundamental principles and mechanics of how it works. Besides that, this article will also highlight the strengths of logistic regression and addresses its limitations, providing a balanced view of its application in modern analytics.
Logistic regression is a statistical method that serves as a powerful tool for predicting binary outcomes based on one or more independent variables. Unlike traditional linear regression, which predicts continuous outcomes, logistic regression is specifically designed for situations where the dependent variable is dichotomous, meaning it can take on only two possible values, such as ‘yes’ or ‘no’, ‘success’ or ‘failure’. This makes it particularly useful in various fields, including healthcare, finance, and social sciences, where decision-making often hinges on binary classifications.

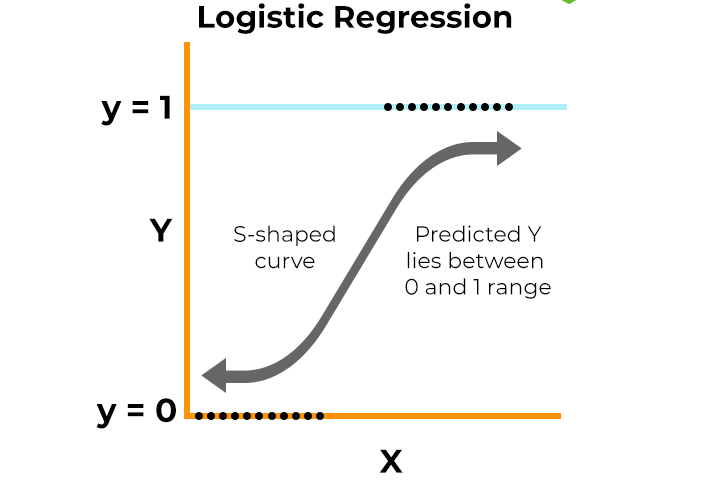
At its core, logistic regression utilizes the logistic function, also known as the sigmoid function, to model the probability of a particular outcome occurring. The defining characteristic of this model is that it transforms the linear combination of the independent variables into a probability score that ranges between 0 and 1. This transformation allows researchers and analysts to interpret the results in terms of odds ratios, providing insights into how changes in the independent variables affect the likelihood of the outcome.
Logistic regression operates on the principle of estimating the probability of a binary outcome based on one or more predictor variables. Unlike linear regression, it uses a logistic function to transform its output into a probability value between 0 and 1. This transformation is achieved through the sigmoid function, which maps any real-valued number into the (0, 1) interval, making it particularly suitable for classification tasks where the dependent variable is dichotomous, such as ‘yes’ or ‘no’, ‘success’ or ‘failure’.

The core mechanics of logistic regression involve calculating the odds of an event occurring and then applying the logistic function to convert these odds into probabilities. The model estimates the relationship between the independent variables and the log-odds of the dependent variable, which is expressed as a linear combination of the predictors. This means that for each predictor, a coefficient is assigned, indicating the strength and direction of its relationship with the outcome. The resulting equation allows for the prediction of probabilities, which can then be thresholded to classify instances into one of the two categories.
Logistic regression is a cornerstone of machine learning, particularly in the realm of classification tasks. As a supervised learning algorithm, it excels at predicting binary outcomes, making it a go-to choice for many data scientists. By estimating the probability that a given input belongs to a particular class, logistic regression provides a clear framework for decision-making.
Moreover, logistic regression can be extended to handle multiclass classification through techniques like one-vs-all or softmax regression. This versatility, combined with its computational efficiency, makes logistic regression a valuable tool in the machine learning toolkit, especially when dealing with large datasets or when interpretability is a priority.
One of the primary advantages is its simplicity; it is straightforward to implement and interpret, making it accessible for practitioners across various fields.
Additionally, it is efficient to train, requiring less computational power compared to more complex algorithms. This efficiency is particularly beneficial when dealing with large datasets, as it allows for quicker model training and evaluation.
Furthermore, logistic regression provides probabilities for outcomes, which can be valuable for decision-making processes, offering insights beyond mere classifications.
One significant drawback is its assumption of linear relationships between the independent variables and the log-odds of the dependent variable, which may not hold true in all scenarios. This can lead to suboptimal performance when dealing with complex datasets that exhibit non-linear relationships.
Additionally, it is limited to binary outcomes, making it unsuitable for multi-class classification problems without modifications.
Lastly, while it performs well with linearly separable data, it may struggle with datasets that require more sophisticated modeling techniques, potentially leading to inaccurate predictions.
In the healthcare sector, for instance, logistic regression is employed to predict patient outcomes, such as the likelihood of disease presence or absence based on diagnostic tests. This predictive capability is crucial for early intervention and treatment planning, making it as a valuable tool for medical professionals.
Additionally, in the realm of finance, it is widely used for fraud detection, where it helps identify potentially fraudulent transactions by analyzing patterns in historical data.
Beyond healthcare and finance, it is also prevalent in marketing, where businesses utilize it to predict customer behavior. By analyzing factors such as demographics and purchasing history, companies can determine the probability of a customer responding positively to a marketing campaign.
Furthermore, logistic regression is instrumental in social sciences, where researchers analyze survey data to understand the relationship between various factors and binary outcomes, such as voting behavior or social issues. Its adaptability to different domains underscores the importance of it in data analysis and decision-making processes.
Logistic regression is a versatile and efficient tool for modeling binary outcomes, widely used across fields like healthcare and finance. Its simplicity, interpretability, and integration into machine learning make it invaluable for classification tasks and data-driven decision-making. While it assumes linearity between predictors and the log-odds, this limitation is often outweighed by its practicality. By understanding its strengths and constraints, users can effectively apply logistic regression to solve complex problems and uncover meaningful insights.