Linear regression is a fundamental statistical method that has gained immense popularity in the field of data analysis and machine learning. It serves as a powerful tool for understanding relationships between variables, making predictions, and uncovering insights from data. As we delve into the intricacies of linear regression, it becomes evident that this technique is not only essential for statisticians but also for professionals across various domains, including finance, healthcare, and marketing.
In this article, we will explore the concept of linear regression, its significance in machine learning, and the key principles that underpin its functionality. We will also examine real-world applications, the challenges practitioners face, and the limitations of this method. By the end of this article, readers will have a well-rounded understanding of linear regression, its advantages, and its potential drawbacks, equipping them with the knowledge to apply this technique effectively in their own work.
Linear regression is a fundamental statistical method used to model the relationship between a dependent variable and one or more independent variables. At its core, it assumes that there is a linear connection between these variables, which can be represented by a straight line in a two-dimensional space. This technique is often referred to as simple regression when it involves a single independent variable, while multiple regression applies when there are several predictors.
The primary goal of this method is to predict the value of the dependent variable based on the known values of the independent variables, making it a powerful tool for data analysis and forecasting. In practical terms, linear regression utilizes a mathematical formula to generate predictions, allowing for easy interpretation of results. The model estimates the coefficients that define the linear relationship, which can then be used to make informed decisions based on the data.
This method is widely recognized for its simplicity and effectiveness, making it one of the most commonly used predictive analysis techniques in various fields, including economics, biology, and social sciences. By establishing a clear relationship between variables, linear regression not only aids in prediction but also helps in understanding the underlying patterns within the data.
At the heart of linear regression lies the concept of establishing a relationship between a dependent variable and one or more independent variables. This relationship is typically represented through a linear equation, which can be expressed in the form of Y = a + bX, where Y is the dependent variable, X is the independent variable, a is the y-intercept, and b is the slope of the line. The slope indicates how much Y changes for a unit change in X, providing a clear interpretation of the relationship. Understanding this equation is crucial, as it forms the foundation for making predictions based on the model.
Another key concept is the distinction between simple and multiple linear regression. Simple linear regression involves a single independent variable, making it easier to visualize and interpret. In contrast, multiple linear regression incorporates two or more independent variables, allowing for a more complex analysis of relationships. This complexity can lead to more accurate predictions, but it also requires careful consideration of multicollinearity, which occurs when independent variables are highly correlated with each other. Additionally, the assumptions underlying linear regression, such as linearity, independence, homoscedasticity, and normality of residuals, are essential for ensuring the validity of the model’s results.
Linear regression is a cornerstone of machine learning, serving as one of the most fundamental supervised learning algorithms for predictive modeling. Its significance lies in its ability to establish a clear relationship between independent and dependent variables, making it an essential tool for data scientists and analysts. By providing a straightforward approach to predicting continuous outcomes, linear regression enables practitioners to derive insights from data efficiently. This simplicity not only aids in understanding complex datasets but also facilitates the communication of results to stakeholders who may not have a technical background.
Moreover, linear regression is widely applicable across various domains, from finance to healthcare, where it is used to forecast trends, assess risks, and evaluate the impact of different factors on outcomes. Its interpretability is a major advantage, as it allows users to understand the influence of each predictor variable on the response variable. This transparency is crucial in fields that require accountability and justification for decisions based on data analysis.
One of the most common uses is in business, where organizations leverage linear regression to analyze the impact of advertising spending on revenue generation. By establishing a clear relationship between these two variables, businesses can make informed decisions about budget allocation and marketing strategies, ultimately driving growth and profitability.
Additionally, linear regression is instrumental in forecasting sales, allowing companies to predict future performance based on historical data, which is crucial for inventory management and resource planning.

In the realm of healthcare, this technique plays a vital role in understanding the relationships between patient characteristics and health outcomes. For instance, researchers may use this technique to analyze how factors such as age, weight, and lifestyle choices influence the likelihood of developing certain medical conditions. This information can guide preventive measures and treatment plans.
Furthermore, linear regression is widely applied in environmental studies, where it helps quantify the effects of variables like temperature, rainfall, and fertilizer usage on agricultural yields. By modeling these relationships, farmers can optimize their practices to enhance productivity and sustainability.
One of the primary concerns of linear regression is its assumption of linearity between the dependent and independent variables. This means that if the true relationship is nonlinear, linear regression may provide misleading results.
Additionally, linear regression assumes that all observations are independent of one another, which can be problematic in cases where data points are correlated, such as in time series data or clustered data. This violation can lead to biased estimates and inflated significance levels, ultimately compromising the model’s reliability.
Another significant limitation is its sensitivity to outliers. Outliers can disproportionately influence the slope of the regression line, leading to skewed results that do not accurately represent the underlying data.
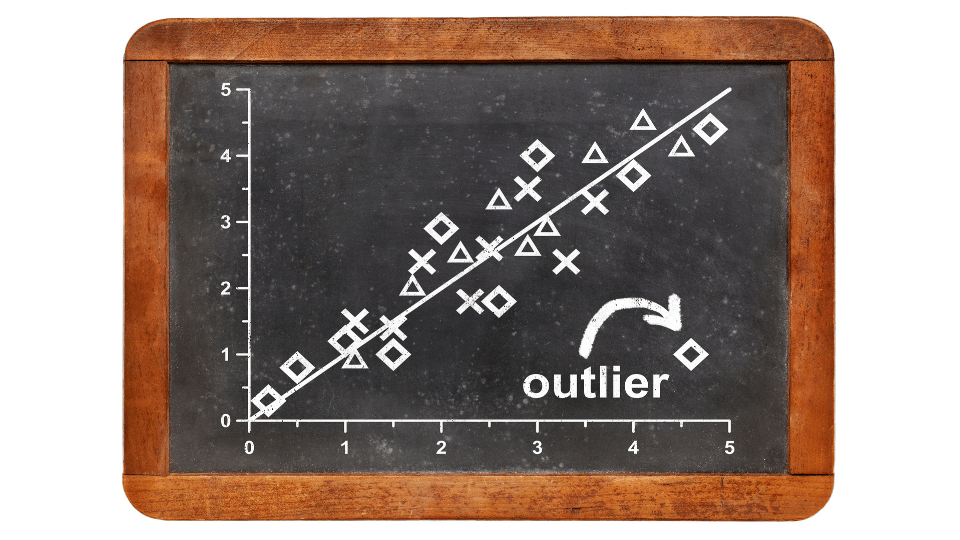
Furthermore, multicollinearity, which occurs when independent variables are highly correlated, can also pose a challenge. It can make it difficult to determine the individual effect of each predictor on the dependent variable, resulting in unstable coefficient estimates.
Linear regression is a fundamental technique in statistics and machine learning, valued for its simplicity and interpretability. While it excels in identifying linear relationships, its limitations include handling non-linearity and multicollinearity. Despite advancements in machine learning, this approach remains a foundational tool for data analysis, offering insights and serving as a benchmark for more complex models. Understanding its strengths and limitations is essential for effective data exploration.